תורת המבחנים הקלאסית
בפסיכולוגיה, מבחנים הם פסיכולוגיים או פסיכו-טכניים ונועדו ללמוד או להעריך פונקציה. לפיכך, מבחנים פסיכולוגיים הם כלים שמעריכים או מודדים את המאפיינים הפסיכולוגיים של נבדק. המשך לקרוא כדי לגלות עוד על תורת המבחנים הקלאסית (CTT).
תיאוריות מבחן
בדיקות הן מכשירי מדידה מתוחכמים. במקרים רבים, הם מועילים להפליא בהקשר של הערכה פסיכולוגית. עם זאת, מבחן חייב לעמוד בציון מספרי פסיכומטרי מינימלי כדי להועיל. בנוסף, המומחה המחיל אותו חייב לדעת את הפרוטוקול לניהולו ולכבד אותו.
מצד שני, תיאוריות המבחן גם אומרות לנו כיצד אנו יכולים להעריך את איכות הבדיקה, ובמקרים רבים, כיצד נוכל לצמצם שגיאות למינימום. במובן זה, אולי שני המושגים החשובים ביותר בתורת המבחנים הקלאסית הם מהימנות ותוקף.
אמינות היא העקביות או היציבות של הנתונים כאשר תהליך המדידה חוזר על עצמו. זו בעצם אוטופיה מכיוון שבפועל, אי אפשר לשחזר את אותם תנאים בשתי מדידות שונות. זה פשוט יחסית לפעול לפי משתנים חיצוניים, כמו לוודא שהטמפרטורה או רמת הרעש זהה לחלוטין. עם זאת, השליטה במשתנים הפנימיים של מי שניגש למבחן היא הרבה יותר קשה.
תוקף מתייחס למידת הראיות והתיאוריה האמפיריות תומכות בפרשנות של ציוני המבחנים (2). אחרת, נוכל לומר שתוקף הוא היכולת של מכשיר מדידה לכמת בצורה משמעותית ומתאימה את מה שהוא נוצר כדי למדוד.
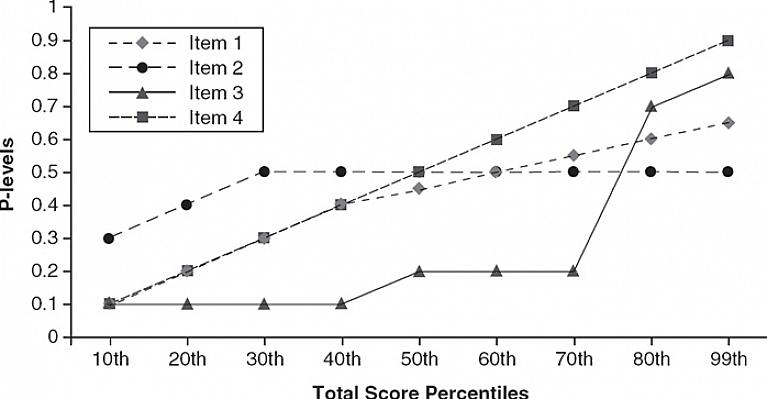
ישנן שתי תיאוריות נהדרות בכל הנוגע לבנייה וניתוח של מבחנים: תורת המבחנים הקלאסית (CTT) ותיאוריית התגובה לפריטים (IRT). להלן, נסביר את ההיבטים המרכזיים של CTT.
תורת המבחנים הקלאסית (CTT)
גישה זו נוטה להיות השימושית ביותר בניתוח ויצירת מבחנים. התשובות שאדם נותן במבחן מושוות באמצעות שיטות סטטיסטיות או איכותניות לתשובות של אנשים אחרים שניגשו לאותו מבחן. זה מאפשר לבצע השוואות.
עם זאת, הסיווג אינו כל כך פשוט. הפסיכולוג, כמו כל איש מקצוע אחר, צריך לוודא שהמכשיר שבו הוא משתמש מכויל במדויק וללא טעויות (1).
לפיכך, כאשר פסיכולוג מחיל מבחן על אדם אחד או כמה, מה שהם משיגים הם הציונים האמפיריים של אותם אנשים. עם זאת, זה לא אומר לנו הרבה על מידת הדיוק של ציונים אלה. לדוגמה, ייתכן שהאדם קיבל ציון נמוך בגלל שהוא לא הרגיש טוב באותו יום או אפילו בגלל שהתנאים הפיזיים של המקום בו ניגשו למבחן לא היו אופטימליים.
מודל רגרסיה ליניארית קלאסית
ספירמן הציע את תורת המבחנים הקלאסית בתחילת המאה ה-20. לאחר מכן הציע החוקר מודל פשוט מאוד עבור ציוני המבחן: מודל רגרסיה ליניארית קלאסית.
מודל זה מורכב מהנחה שלציון מבחן מסוים או ל"ציון אמפירי" (X) יש שני משתנים. המשתנה הראשון הוא הציון האמיתי (V) והשני הוא השגיאה (e). זה האחרון עלול להיגרם על ידי דברים שאינם בשליטתנו. זו הסיבה ש-CTT אחראית לקביעת טעות המדידה.
הנוסחה שלו היא: X = V + e
לאחר מכן, ספירמן הוסיפה שלוש הנחות למודל:
שלוש ההנחות של מודל הרגרסיה הליניארית הקלאסי
- הציון האמיתי (V) הוא הציפייה המתמטית של הציון האמפירי: V = E (X).
- לפיכך, ציון המבחן האמיתי של אדם הוא הציון הממוצע של אותו מבחן אם מישהו היה עובר אותו ללא סוף.
- אין קשר בין מספר הציונים האמיתיים לבין השגיאות המשפיעות על הציונים הללו: r (v, e) = 0
- הציון האמיתי אינו תלוי בטעות המדידה.
- שגיאות המדידה בבדיקה מסוימת אינן קשורות לשגיאות המדידה בבדיקה אחרת: r (ex, ek) = 0
- שגיאות שנעשו בהזדמנות אחת לא ישתוו לאלה שנעשו בבדיקה אחרת.
תורת המבחנים הקלאסית היא פשוטה. ניתן ליישם אותו בכל הקשר ולהוציאו לפועל ללא צורך במיומנויות מתמטיות מתקדמות במיוחד. עם זאת, הבעיה היא שהתוצאות שהיא מניבה תמיד יהיו קשורות לאוכלוסיה שבה הבדיקה אומתה. בנוסף, המבחנים דורשים ציון מינימלי מקובל.